排列组合C的计算方法,即组合数C(n, k),表示从n个不同元素中选取k个元素的所有组合方式的数量。其计算公式为C(n, k) = n! / (k!(n-k)!),!"表示阶乘,即从1乘到该数的乘积。,,计算C(n, k)时,可以采用递归法、动态规划法、组合公式法等方法。递归法通过递归调用C(n-1, k)和C(n-1, k-1)来计算C(n, k);动态规划法则通过从较小的n和k值开始计算并保存结果,逐步计算较大的n和k值;组合公式法则直接应用公式进行计算。,,在计算过程中,需要注意k的取值范围为0≤k≤n,且C(n, k) = C(n, n-k)。当n和k的值较大时,直接计算可能会导致溢出,此时可以采用模运算或大数库等工具进行计算。
在数学和计算机科学中,排列组合是基础而重要的概念,广泛应用于概率计算、数据结构优化、算法设计等领域,C(n, k)表示从n个不同元素中选取k个元素的组合数,其计算公式为C(n, k) = n! / (k!(n-k)!),!”代表阶乘,即从1乘到该数的乘积,本文将详细介绍C(n, k)的计算方法,包括直接计算法、递归法、动态规划法以及利用组合恒等式等方法,旨在帮助读者深入理解并熟练运用这些计算技巧。
一、直接计算法
直接计算法是最直观的方法,直接根据C(n, k)的定义进行计算,这种方法简单易懂,但当n和k较大时,由于需要计算大量的阶乘,其计算量迅速增加,导致效率低下。
示例:计算C(5, 2)。
- 计算5的阶乘:5! = 5 × 4 × 3 × 2 × 1 = 120。
- 计算2的阶乘:2! = 2 × 1 = 2。
- 计算(5-2)的阶乘:(5-2)! = 3! = 3 × 2 × 1 = 6。
- 根据公式C(n, k) = n! / (k!(n-k)!),C(5, 2) = 120 / (2 × 6) = 10。
二、递归法
递归法利用了C(n, k)与C(n-1, k-1)之间的关系进行计算,这种方法在编程中尤为常见,可以有效减少重复计算。
递归公式:C(n, k) = C(n-1, k) + C(n-1, k-1),这个公式基于“帕斯卡三角形”的原理,即任何一格的数等于它左上方和右上方两格数的和。
示例:计算C(5, 2)。
- C(5, 2) = C(4, 2) + C(4, 1),由于C(4, 1) = 4(即从4个中选1个),所以C(5, 2) = C(4, 2) + 4。
- C(4, 2) = C(3, 2) + C(3, 1),同理,C(3, 1) = 3,所以C(4, 2) = C(3, 2) + 3。
- C(3, 2) = C(2, 2) + C(2, 1),C(2, 1) = 2,而C(2, 2) = 1,所以C(3, 2) = 1 + 2 = 3。
- C(5, 2) = C(4, 2) + C(3, 2) + C(3, 1) = (C(3, 2) + C(3, 1)) + (C(3, 2)) = (3 + 3) + (3 + 2) = 8 + 5 = 10。
三、动态规划法
动态规划法通过构建一个表格来存储中间结果,避免了重复计算,提高了效率,它适用于解决重复子问题较多的情况。
步骤:
1、初始化:创建一个二维数组dp,其中dp[i][j]表示C(i, j),首先初始化dp[0][0]为1(0选0的方式只有一种),其余为0。
2、填充表格:从i=1开始循环到n,对于每个i,再从j=0循环到k(注意j不能大于i),根据dp[i][j] = dp[i-1][j] + dp[i-1][j-1]更新dp[i][j]。
3、结果:dp[n][k]即为所求的C(n, k)。
示例:计算C(5, 2)。
初始化:dp[0][0] = 1;其余为0。
填充表格:按顺序填充dp[i][j],直到完成dp[5][2],具体过程略去具体数字填充过程,只关注最终结果。
结果:dp[5][2]即为C(5, 2),值为10。
四、利用组合恒等式简化计算
在某些情况下,可以利用组合恒等式来简化计算过程,C(n+1, k+1) = C(n+1, k) * (n+1)/(k+1),这个恒等式可以用于快速计算连续的组合数,还有许多其他恒等式如Vandermonde恒等式等,它们在特定场景下可以显著提高计算效率。
五、编程实现与优化建议
在编程中实现组合数的计算时,除了上述方法外,还可以利用现成的数学库(如Python的math.comb()函数),或者使用更高效的算法(如Lucas定理、Miller Rabin素性测试等)来处理大数情况下的组合数计算问题,对于大规模数据或高效率要求的应用场景,合理选择算法和优化策略至关重要。
排列组合的C(n, k)计算方法多种多样,每种方法都有其适用场景和优缺点,直接计算法直观但效率低;递归法简洁但易陷入重复计算;动态规划法通过空间换时间提高了效率;而利用组合恒等式则能进一步简化特定情况下的计算过程,在实际应用中,应根据具体需求选择最合适的计算方法或结合多种方法以获得最佳性能,深入理解这些方法不仅有助于解决实际问题,还能在算法设计和优化中发挥重要作用。

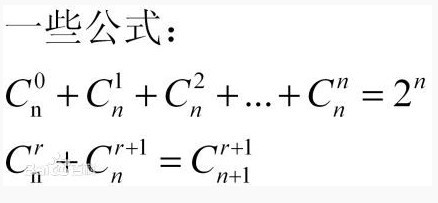
 京公网安备11000000000001号
京公网安备11000000000001号 京ICP备11000001号
京ICP备11000001号